Gradient flow in neural networks
November 11, 2025
Revisiting Andrej Karpathy’s vanishing gradients post (it was trending on Hacker News recently) got me thinking about how easy/difficult it is to see vanishing/exploding gradients from computational graphs versus math equations.
I’ve always been on the side that computational graphs are easier to understand and reason about than strewn out hideous math equations. But this may be the one case where it’s actually easier to understand something by looking at the math equations!
1 layer neural network
For simplicity, we’ll be looking at 1D neural networks.
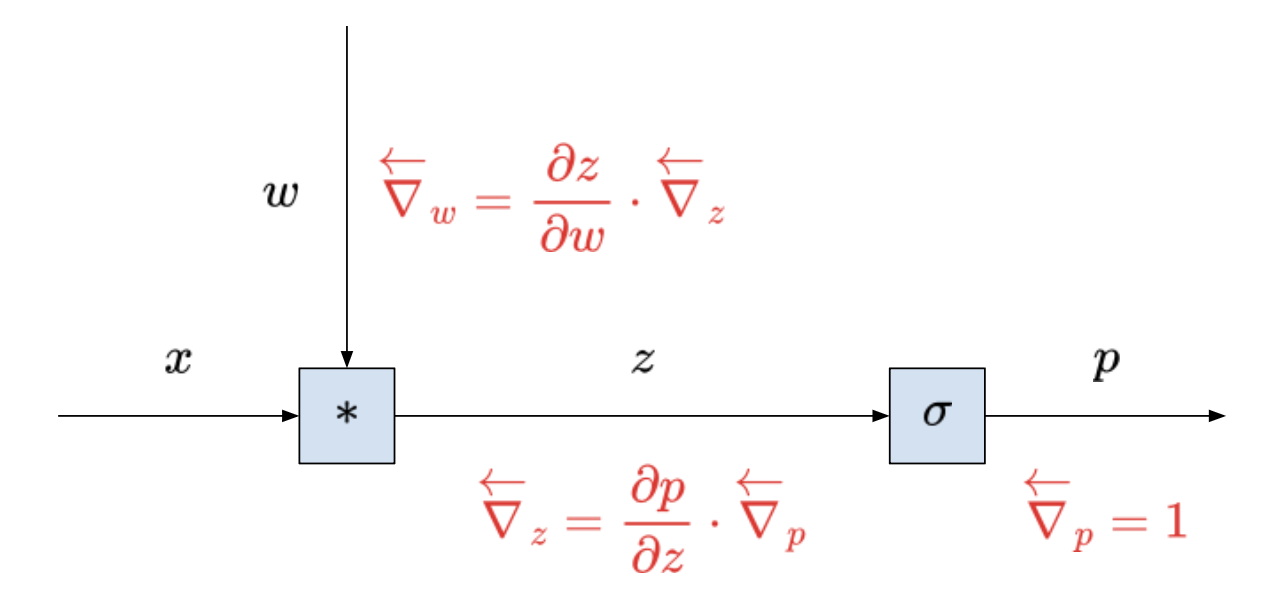
This is a picture of the gradient flow from $p$ to $w$. It’s pretty great for locally computing and propagaing the gradient backward, one step at a time. Though, it’s pretty hard to see just by looking at the computational graph why the gradient could explode or vanish!
But if we write out the equation:
\[\begin{align} \frac{\partial p}{\partial w} &= \frac{\partial z}{\partial w} \cdot \frac{\partial p}{\partial z} \\ &= x \cdot p (1 - p) \end{align}\]Granted we only have two terms. But they’re being multiplied! And multiplication is an operation that can scale things up or down down pretty quickly. So we can begin to see how our gradient might become very large or very small!
2 layer neural network
Okay, it’s easier to see the deeper the neural net gets:
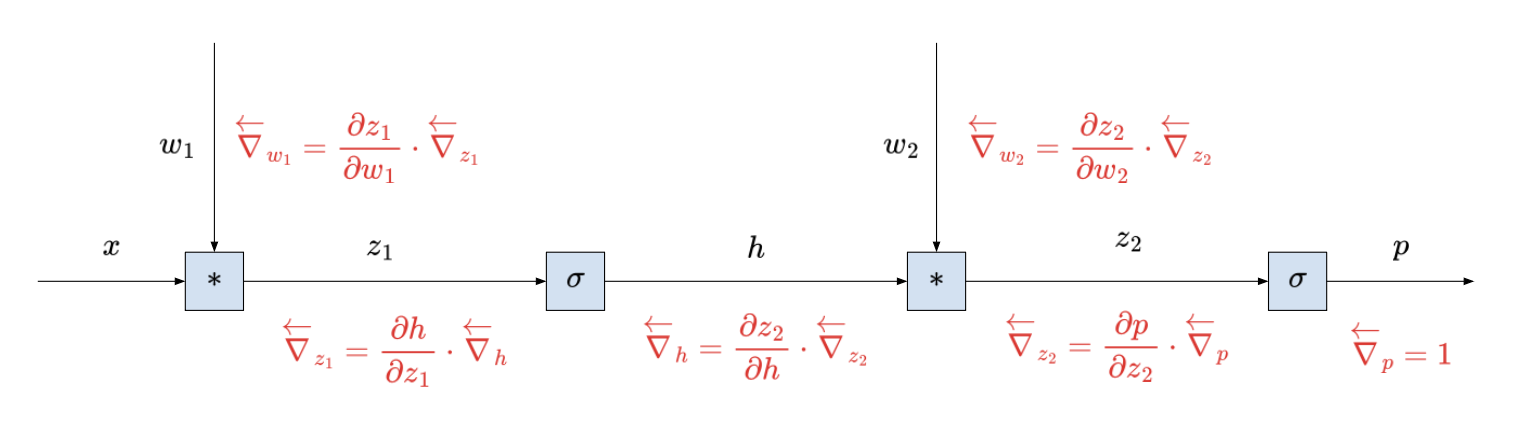
Again, it’s not super easy to see that the gradient would explode or vanish just by looking at the computational graph - you’ve just got a bunch of local terms.
But if we write out the equation:
\[\begin{align} \frac{\partial p}{\partial w_1} &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial p}{\partial z_1} \\ &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial h}{\partial z_1} \cdot \frac{\partial p}{\partial h} \\ &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial h}{\partial z_1} \cdot \frac{\partial z_2}{\partial h} \cdot \frac{\partial p}{\partial z_2} \\ &= x_1 \cdot z_1 (1 - z_1) \cdot w_2 \cdot z_2 (1 - z_2) \end{align}\]Look at that - you’ve got a product of a bunch of terms! And that could blow up or diminish pretty quickly!
Math’s compact nature here is actually do a pretty great job providing a representation that allows us to see the global structure.
3 layer neural network
Let’s look at one more neural net just for kicks - a three layer net:

Again, could you tell the gradient might explode or vanish just by looking at this graph?
But looking at the math:
\[\begin{align} \frac{\partial p}{\partial w_1} &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial p}{\partial z_1} \\ &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial h_1}{\partial z_1} \cdot \frac{\partial p}{\partial h_1} \\ &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial h_1}{\partial z_1} \cdot \frac{\partial z_2}{\partial h_1} \cdot \frac{\partial p}{\partial z_2} \\ &= \frac{\partial z_1}{\partial w_1} \cdot \frac{\partial h_1}{\partial z_1} \cdot \frac{\partial z_2}{\partial h_1} \cdot \frac{\partial h_2}{\partial z_2} \cdot \frac{\partial z_3}{\partial h_2} \cdot \frac{\partial p}{\partial z_3} \\ &= x \cdot z_1 (1 - z_1) \cdot w_2 \cdot z_2 (1 - z_2) \cdot w_3 \cdot z_3 (1 - z_3) \end{align}\]I think you get the point - every time the net gets deeper we’re throwing more terms into an ever-expanding product.
Conclusion
Computational graphs are great! But they aren’t the best representation for understanding absolutely everything when it comes to gradient flow in neural networks.
I hope this post has helped you to see a bit more clearly why vanishing and exploding gradients might occur!